Teorema del valor medio
De Wikipedia, la enciclopedia libre
En cálculo diferencial, el teorema de valor medio (de Lagrange) teorema de los incrementos finitos', teorema de Bonnet-Lagrange o teoría del punto medio es una propiedad de las funciones derivables en un intervalo. Algunos matemáticos consinte que une los puntos (a, f(a)) y (b, f(b)). Es decir:
El teorema del valor medio de Lagrange de hecho es una generalización del teorema de Rolle que dice que si una función es definida y continua [ a , b ], diferenciable en el intervalo abierto ( a , b ) , y toma valores iguales en los extremos del intervalo --en otras palabras, f ( a ) = f ( b )-- entonces existe al menos algún punto c en el intervalo ( a , b ) tal que la tangente a la curva en c es horizontal, es decir f '( c)=0.Demostración
El conocimiento del significado de la derivada de una función en un punto, y de la ecuación punto-pendiente de una recta, permiten deducir que la ecuación de la recta tangente en un punto de la curva es:
 y
y  son una pareja cualquiera de puntos de la curva. Vamos a demostrar que, una vez conocida una pareja de puntos de una curva continua y derivable, existe un punto c contenido en el intervalo (a,b) tal que la pendiente en dicho punto es paralela a la recta que une los puntos (a, f(a)) y (b, f(b)). Definimos una función:
son una pareja cualquiera de puntos de la curva. Vamos a demostrar que, una vez conocida una pareja de puntos de una curva continua y derivable, existe un punto c contenido en el intervalo (a,b) tal que la pendiente en dicho punto es paralela a la recta que une los puntos (a, f(a)) y (b, f(b)). Definimos una función:
 en el intervalo
en el intervalo ![[a,b]](http://upload.wikimedia.org/wikipedia/es/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) , existe un valor
, existe un valor  en dicho intervalo, tal que[1]
en dicho intervalo, tal que[1]
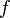 es continua en
es continua en ![[a,b]](http://upload.wikimedia.org/wikipedia/es/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) , posee un valor máximo en dicho intervalo para algún
, posee un valor máximo en dicho intervalo para algún ![V\in[a,b]](http://upload.wikimedia.org/wikipedia/es/math/4/a/1/4a1e1d14937d04326d7a845e7fa35910.png) , que llamaremos
, que llamaremos  y también un valor mínimo en el mismo intervalo:
y también un valor mínimo en el mismo intervalo:  , para algún
, para algún ![v\in[a,b]](http://upload.wikimedia.org/wikipedia/es/math/3/b/3/3b312e38b04fbf597f3b9eca8c6e5040.png) . Es decir
. Es decir ![f(V)\geq f(x),\forall x\in[a,b]](http://upload.wikimedia.org/wikipedia/es/math/5/c/8/5c872c61f74b1ed1dc2c15ddc1b73096.png) y
y ![f(v)\leq f(x),\forall x\in[a,b]](http://upload.wikimedia.org/wikipedia/es/math/2/2/1/221e994f5c5d64bda66f5407876d2106.png) . Si consideramos las áreas de los rectángulos con base
. Si consideramos las áreas de los rectángulos con base  y altura
y altura  ó
ó  tendremos la siguiente desigualdad:
tendremos la siguiente desigualdad:
![\xi\in[a,b]](http://upload.wikimedia.org/wikipedia/es/math/f/8/3/f83ba3f626ed0ec9d1df2f3139d398d0.png) para el cual la función
para el cual la función 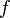 alcanza el valor de la integral
alcanza el valor de la integral  , es decir:
, es decir:
 , pero resulta que
, pero resulta que 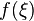 coincide con el valor medio (promedio) de la función
coincide con el valor medio (promedio) de la función 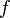 en el intervalo
en el intervalo ![[a,b]](http://upload.wikimedia.org/wikipedia/es/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
.
 un conjunto abierto y convexo y
un conjunto abierto y convexo y  una función real diferenciable sobre ese abierto. Entonces se tiene que:[2]
una función real diferenciable sobre ese abierto. Entonces se tiene que:[2]
 . En este caso, sólo es posible establecer la siguiente desigualdad en términos de la norma:
. En este caso, sólo es posible establecer la siguiente desigualdad en términos de la norma:
Este teorema lo formuló Lagrange.
El teorema del valor medio de Lagrange de hecho es una generalización del teorema de Rolle que dice que si una función es definida y continua [ a , b ], diferenciable en el intervalo abierto ( a , b ) , y toma valores iguales en los extremos del intervalo --en otras palabras, f ( a ) = f ( b )-- entonces existe al menos algún punto c en el intervalo ( a , b ) tal que la tangente a la curva en c es horizontal, es decir f '( c)=0.Demostración
El conocimiento del significado de la derivada de una función en un punto, y de la ecuación punto-pendiente de una recta, permiten deducir que la ecuación de la recta tangente en un punto de la curva es:
Donde los pares de puntos
 y
y  son una pareja cualquiera de puntos de la curva. Vamos a demostrar que, una vez conocida una pareja de puntos de una curva continua y derivable, existe un punto c contenido en el intervalo (a,b) tal que la pendiente en dicho punto es paralela a la recta que une los puntos (a, f(a)) y (b, f(b)). Definimos una función:
son una pareja cualquiera de puntos de la curva. Vamos a demostrar que, una vez conocida una pareja de puntos de una curva continua y derivable, existe un punto c contenido en el intervalo (a,b) tal que la pendiente en dicho punto es paralela a la recta que une los puntos (a, f(a)) y (b, f(b)). Definimos una función:Puesto que f es continua en [a, b] y diferenciable en (a, b), lo mismo se puede decir de g. Además g satisface las condiciones del Teorema de Rolle ya que:
Por el Teorema de Rolle, como g es derivable en (a, b) y g(a)=g(b), existe un c perteneciente (a, b) tal que g '(c) = 0, y por tanto:
y así
como queríamos demostrar.
[editar] Forma integral del Teorema del valor medio
Para una función continua en el intervalo
en el intervalo ![[a,b]](http://upload.wikimedia.org/wikipedia/es/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) , existe un valor
, existe un valor  en dicho intervalo, tal que[1]
en dicho intervalo, tal que[1]Demostración Dado que la función
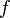 es continua en
es continua en ![[a,b]](http://upload.wikimedia.org/wikipedia/es/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) , posee un valor máximo en dicho intervalo para algún
, posee un valor máximo en dicho intervalo para algún ![V\in[a,b]](http://upload.wikimedia.org/wikipedia/es/math/4/a/1/4a1e1d14937d04326d7a845e7fa35910.png) , que llamaremos
, que llamaremos  y también un valor mínimo en el mismo intervalo:
y también un valor mínimo en el mismo intervalo:  , para algún
, para algún ![v\in[a,b]](http://upload.wikimedia.org/wikipedia/es/math/3/b/3/3b312e38b04fbf597f3b9eca8c6e5040.png) . Es decir
. Es decir ![f(V)\geq f(x),\forall x\in[a,b]](http://upload.wikimedia.org/wikipedia/es/math/5/c/8/5c872c61f74b1ed1dc2c15ddc1b73096.png) y
y ![f(v)\leq f(x),\forall x\in[a,b]](http://upload.wikimedia.org/wikipedia/es/math/2/2/1/221e994f5c5d64bda66f5407876d2106.png) . Si consideramos las áreas de los rectángulos con base
. Si consideramos las áreas de los rectángulos con base  y altura
y altura  ó
ó  tendremos la siguiente desigualdad:
tendremos la siguiente desigualdad:Lo que implica:
De donde se deduce que debe existir algún
![\xi\in[a,b]](http://upload.wikimedia.org/wikipedia/es/math/f/8/3/f83ba3f626ed0ec9d1df2f3139d398d0.png) para el cual la función
para el cual la función 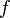 alcanza el valor de la integral
alcanza el valor de la integral  , es decir:
, es decir:El teorema no especifíca como determinar
 , pero resulta que
, pero resulta que 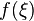 coincide con el valor medio (promedio) de la función
coincide con el valor medio (promedio) de la función 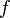 en el intervalo
en el intervalo ![[a,b]](http://upload.wikimedia.org/wikipedia/es/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
.[editar] Enunciado para varias variables
Sea un conjunto abierto y convexo y
un conjunto abierto y convexo y  una función real diferenciable sobre ese abierto. Entonces se tiene que:[2]
una función real diferenciable sobre ese abierto. Entonces se tiene que:[2]Donde:
[editar] Generalizaciones
No existe un análogo estricto del teorema de valor medio para aplicaciones . En este caso, sólo es posible establecer la siguiente desigualdad en términos de la norma:
. En este caso, sólo es posible establecer la siguiente desigualdad en términos de la norma:

![g(x)= f(x) - y = f(x) - [f(a) + \frac{f(b)-f(a)}{b-a}(x-a)]](http://upload.wikimedia.org/wikipedia/es/math/8/f/c/8fc5aba0acb4288e7d4d60688ad1a6d6.png)






![\exists \xi\in[a,b]:\quad f(\xi)=\frac{1}{(b-a)}\int_{a}^{b}f(x)dx](http://upload.wikimedia.org/wikipedia/es/math/b/9/4/b946e39871e427817893ebf0058941a4.png)
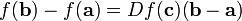
 , es la aplicación lineal que representa el
, es la aplicación lineal que representa el 


No hay comentarios:
Publicar un comentario